Ruth N Bolton & Randall G Chapman (1986) Searching for Positive Returns at the Track: A Multinomial Logit Model for Handicapping Horse Races
Summary
This paper investigates fundamental investment strategies to detect and exploit the public’s systematic errors in horse race wager markets. A handicapping model is developed and applied to win-betting in the pari-mutuel system. A multinomial logit model of the horse racing process is posited and estimated on a data base of 200 races. A recently developed procedure for exploiting the information content of rank ordered choice sets is employed to obtain more efficient parameter estimates. The variables in this discrete choice probability model include horse and jockey characteristics, plus several race-specific features. Hold-out sampling procedures are employed to evaluate wagering strategies. A wagering strategy that involves unobtrusive bets, with a side constraint eliminating long-shot betting, appears to offer the promise of positive expected returns, even in the presence of the typically large track take encountered at Thoroughbred racing events.
Motivation
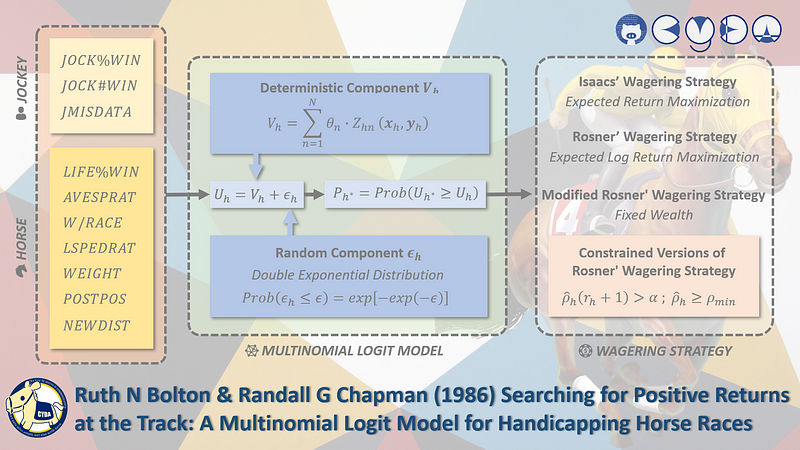
Ruth Bolton indicated that if the public makes systematic and detectable errors in establishing the betting odds, it may be possible to exploit such a situation with a superior wagering strategy and make wagers with a positive expected rate of return. However, academic researchers are all focusing evaluating the efficiency of horse race wager markets. Therefore, she promoted a two-components wagering system having a model of the horse race process and a wagering strategy.
A model of the horse race process attempts to predict the outcome of a race which main output is a prediction of the probabilities of each horse winning a race
A wagering strategy uses the probabilities as inputs to a betting algorithm which determines the amounts to wager on each horse
The Pari-Mutuel System

The Stochastic Utility Model

Model Parameters Estimation

Ruth Bolton indicated that the first three finishers typically receive a portion of the purse and it seems reasonable to assume that those horses and their jockeys are trying and that their finishing position reflects well on their relative “worths”.
For exploiting rank ordered choice set, please refer
- Exploiting Rank Ordered Choice Set Data Within the Stochastic Utility Model (Chapman, Randall & Staelin, Richard, 1982)
- Preference, Utility, and Subjective Probability (Luce, R. D. and Suppes, P., 1965)
Race Data Required
- There are in total 200 races observed from the Daily Racing Form.
- Each race satisfied the following restrictions:
(i) the race was run over good or fast tracks
(ii) the race distance was in the 1–1.25 mile range
(iii) each horse in the race was a separate betting entry
(iv) the horses were at least three years of age
Features Selection
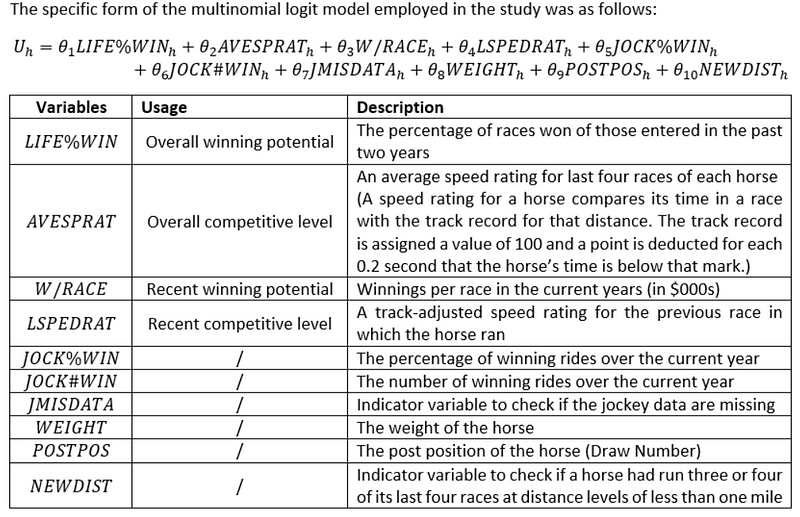
Features Interpretation
- AVESPRAT accounts for the most variation in the model.
- W/RACE appears to be more important than LIFE%WIN.
- WEIGHT does not seem to be an important determinant of finishing position given the presence of the other variables in the model.
- POSTPOS and NEWDIST appear to exhibit nontrivial effects on winning probabilities.
- The jockey variables appear to have less overall importance than the horse’s attributes in determining winning probabilities although this finding may be due to collinearity among the horse and jockey variables.
Model Validity
According to Ruth Bolton, this model has substantial face validity on several dimensions.
- The multinomial logit model considers the competitive nature of the horse racing process. The choice probability expression explicitly includes the characteristics of each horse in comparison with all other horses in a specific race and not relative to all horses in the universe.
- An intuitively appealing theoretical utility maximizing framework was utilized in developing the model.
- The empirical results indicate that the model operationalization passes the usual tests of statistical significance. The empirical findings are consistent with a priori theoretical beliefs. However, it remains to be determined whether this model is sufficiently accurate to allow for the development of a superior wagering system which will earn positive returns.
Wagering Strategy
Ruth Bolton introduced two classes of wagering strategies: algorithms involving multiple bets per race and algorithms involving a single bet per race.
An optimal set of wagers can be derived from a variety of wagering strategies based on different objective functions. For example, a wagering algorithm based on expected value maximization might be appropriate for a risk neutral bettor. Alternatively, an algorithm that maximizes expected log returns would be consistent with risk averse behavior.
Isaacs’ Wagering Strategy
Ruth Bolton mentioned Isaacs’ Wagering Strategy which used to determine the optimal amounts to wager for a risk neutral bettor with infinite wealth. She indicated that it is necessary to assume that the expected value maximizing bettor is the last bettor.
Four Factors for Issacs’ Wagering Algorithm:
- The true winning probabilities
- The public’s consensus probabilities
- The size of the track take
- The size of the betting pool
However, the average return per race was -39.5%. It is because the modest errors in the estimates of the true winning probabilities could cause substantial deviations from the optimal return of Issacs’ strategy.
Therefore, Issac’s strategy is unlikely to be profitable unless the estimates of the true winning probabilities are sufficiently accurate.
Rosner’ Wagering Strategy
Another strategy Ruth Bolton mentioned was Rosner’ Wagering Strategy which used to determine the optimal amounts to wager for a risk averse bettor. The assumption was that the wagers have no effect on the odds.
However, the average return per race was -14.1%. It is because of two problems. First, the bettor’s wagers in a given race can be large enough to significantly affect the track odds. Second, large fluctuations in wealth from race to race lead to considerable variability in the size of the bettor’s wagers per race.
Modified Rosner’ Wagering Strategy
The modified strategy was utilized to make the wagers less obtrusive and to remove the effect of race sequence on the return across races. Practically speaking, Ruth Bolton suggested the wealth to be fixed and equal to $1000 for each race and the bettor wagers some fraction of this amount. The average return across 50 races was -6.4%.
However, this strategy came up of two problems. First, returns were somewhat overestimated because they do not take into account the effect of the wagers on the track odds. Second, returns may be underestimated because the modification to Rosner’s wagering strategy is sub-optimal in the sense that it no longer maximizes the long run rate of asset growth.
Constrained Versions of Rosner’ Wagering Strategy
There were in total two constraints so as to avoid those wagers with low or negative actual returns.
- The strategy suggested that the bettor should wager only on horse with estimated expected returns which are substantially greater than one. Ruth Bolton tested on the value range from 1.0 and 1.8 in increments of 0.1. 50% of the wagers are eliminated at value equals 1.8.
- The bettor should wager only if the estimated probabilities not less than a specified minimum winning probabilities estimate. In the test, the specified estimate would be between 0.00 and 0.25 in increments of 0.01. For reference, when the specified estimate set as 0.12, 55% of the bets are eliminated.
With this strategy, Ruth Bolton claimed to yield a POSITIVE average return.
Words From Editor
As a matter of fact, Ruth Bolton did an incredible work and it stunned me considering the computing power and how difficult to collect data at 1980s. However, to be honest, I would say this research paper is a little bit outdated and not practical at all.
The whole article illustrated the formula of multinomial logit model in detail. It also limited to produce a certain level of complexity of the estimations due to the computational power. Nowadays, we can easily import the library and construct a multinomial logit model with the full set of estimated figures. Therefore, I would say this paper to be an optional article for those mathematics enthusiasts.
For me, I do like the constraints that Ruth Bolton suggested. I think most of us can think of the first constraint by ourselves which is to ensure the estimated expected return to be greater than 1. However, the second constraint is destructive and useful. This idea is sharing the same concept of one of my own wagering strategies which is eliminating the options that are greater than a specific odds level. (personally speaking, I choose the maximum value in five number summary of the odds for the past winning horses)

Comments
Post a Comment